1.9: Diffusion - Chemistry LibreTexts
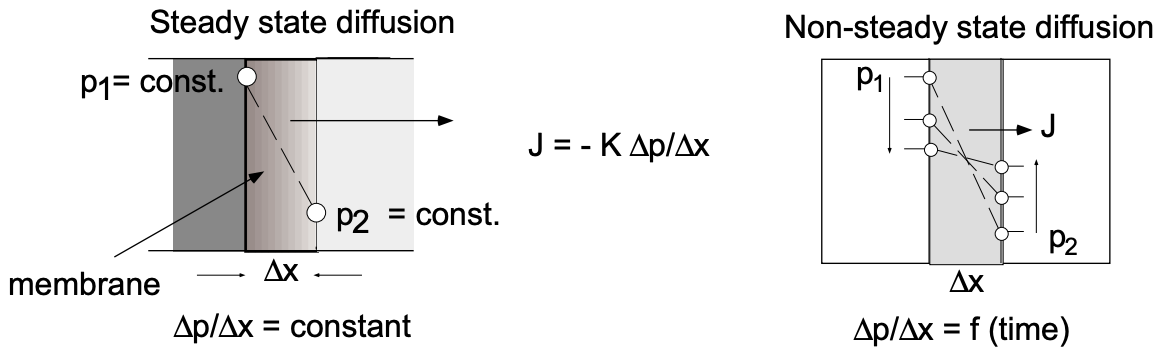
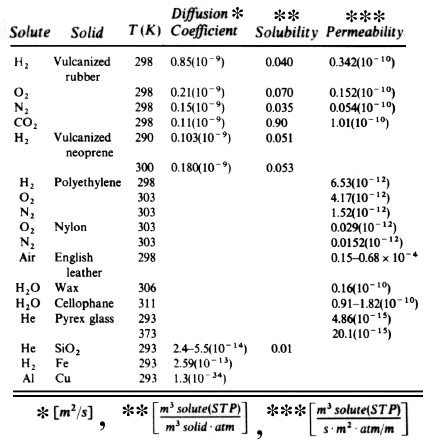
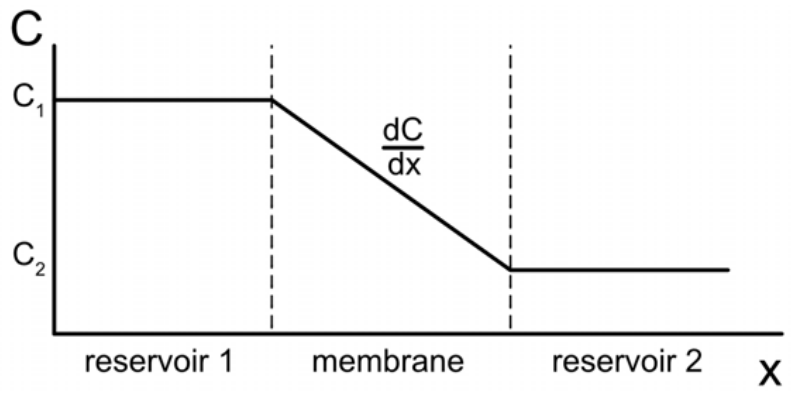
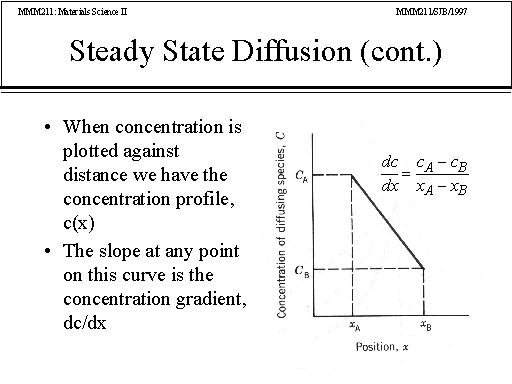
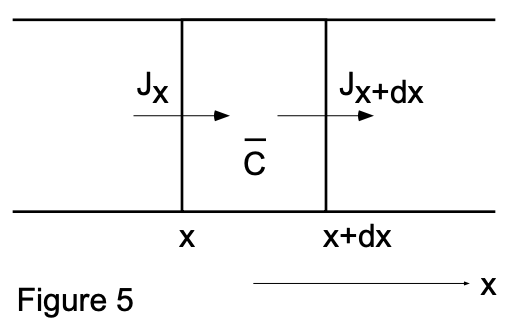
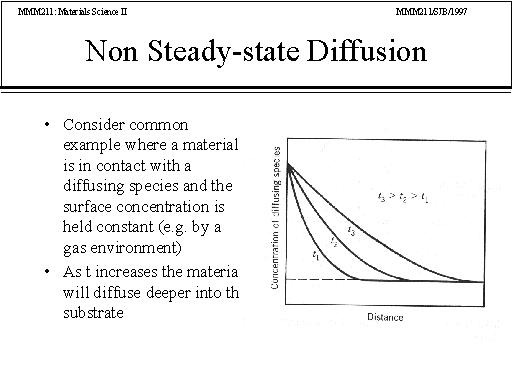
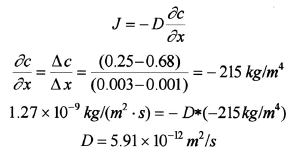SOLVED: A problem similar to the heat transfer example discussed in class results from steady-state mass balance for a chemical in a one-dimensional canal: dc/dc + U * (d^2c/dx^2) = 0 where
EXAMPLE PROBLEMS
Solved 3. Non-steady state diffusion can be described by the | Chegg.com
Diffusion Chapter 5 9/4/2019 9:52 AM9/4/2019 9:52 AM - ppt download
Anomalous diffusion in a variable area whose boundary moves with a constant speed
Chapter 5: Diffusion 5.1 Steady-State Diffusion
Diffusion in Solids, Liquids, and Gases - GeeksforGeeks
Fick's laws of diffusion - Wikipedia
6.26: Steady State Diffusion, Diffusion Coefficient, Fick's Second Law - Chemistry LibreTexts
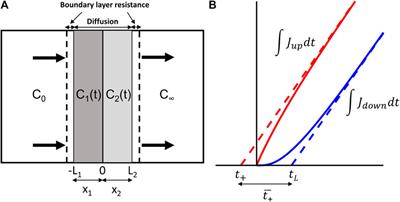
Frontiers | Transient Diffusion in Bi-Layer Composites With Mass Transfer Resistance: Exact Solution and Time Lag Analysis
Jason Montaner's example problems for diffusion.
Fick's First Law of Diffusion | Equation & Example - Lesson | Study.com
![SOLVED: Consider the steady-state convection-diffusion equation in one-dimensional space: (a(c) * d^2u(r)/dx^2) + b(r) * du(l(c))/dx = f(c), for x € [0, 1] with boundary conditions u(0) = u(1) = 0. Here,](https://cdn.numerade.com/ask_images/b5b326f1712c465a855f999c11bfeeed.jpg "SOLVED: Consider the steady-state convection-diffusion equation in one-dimensional space: (a(c) * d^2u(r)/dx^2) + b(r) * du(l(c))/dx = f(c), for x € [0, 1] with boundary conditions u(0) = u(1) = 0. Here,")
SOLVED: Consider the steady-state convection-diffusion equation in one-dimensional space: (a(c) * d^2u(r)/dx^2) + b(r) * du(l(c))/dx = f(c), for x € [0, 1] with boundary conditions u(0) = u(1) = 0. Here,
Lesson 3 Homework Solutions - MATSE 259 Summer 2016 Lesson 3: Diffusion Practice Problem Solutions - Studocu
Solved Thank you very much for solving this problem, I think | Chegg.com
Answered: Non Steady State Diffusion (NSSD)… | bartleby
PPT - CHAPTER 5: DIFFUSION IN SOLIDS PowerPoint Presentation, free download - ID:6123584
Steady State Diffusion (cont.)
Solved Nx zaL Problem 4 - Steady-state diffusion: irregular | Chegg.com
1.9: Diffusion - Chemistry LibreTexts
Non Steady-state Diffusion
Example 3: Steady-state diffusion equation for | Chegg.com
PPT - CHAPTER 5: DIFFUSION IN SOLIDS PowerPoint Presentation, free download - ID:6123584
Diffusion: Chapter 6.
