Chapter 8 Diffusion Equation
Diffusion Equation | Definition & Solution | nuclear-power.com
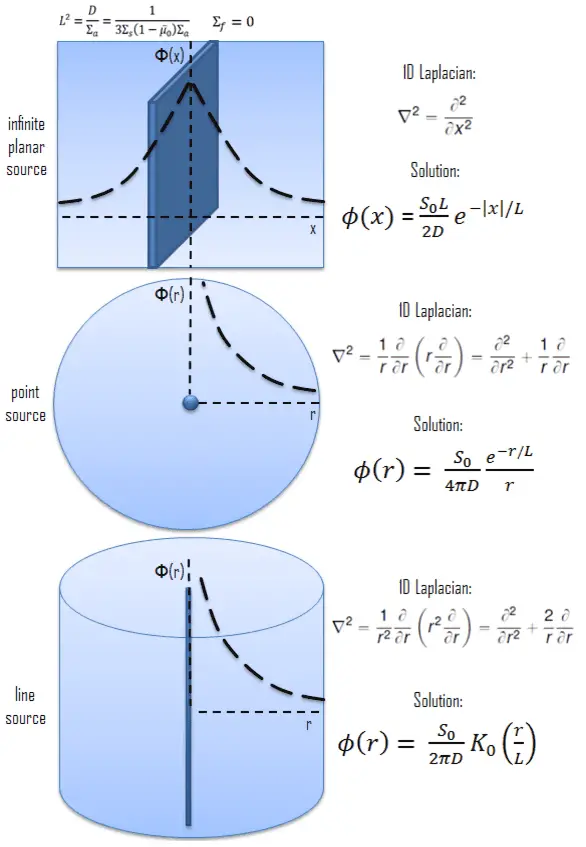
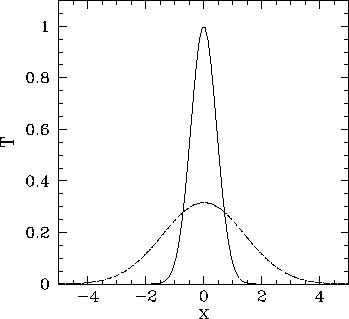
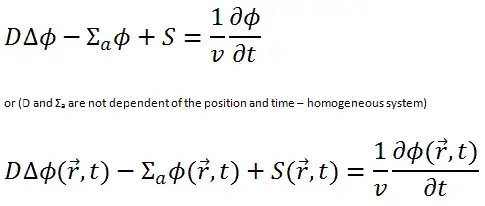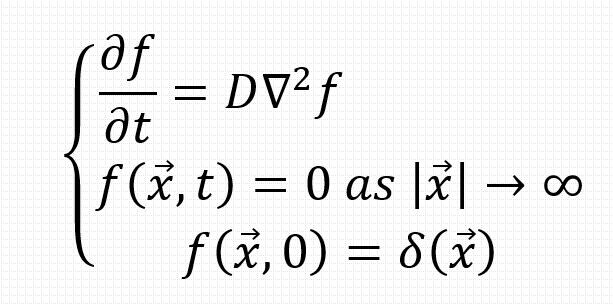Figure 4 from Analytical Solution to the One-Dimensional Advection-Diffusion Equation with Temporally Dependent Coefficients | Semantic Scholar
Fundamental solution of diffusion equation in two | Chegg.com
Math: Partial Differential Eqn. - Ch.1: Introduction (38 of 42) The Diffusion Equation (Part 1 of 5) - YouTube
Numerical Solution of the Diffusion Equation with Constant Concentration Boundary Conditions
3. 1D Second-order Linear Diffusion - The Heat Equation — The Visual Room
Solve 2d diffusion equation | iMechanica
Solution of fourth order semilinear diffusion equation with diffusion... | Download Scientific Diagram
![SOLVED: 6.17 Write a MATLAB code to solve the diffusion equation dx^2 over the domain x ∈ [0, 1] subject to dc/dx(0,x) = d^2c/dx^2(0,x) = 0 (0) for the (dimensionless) reaction rate](https://cdn.numerade.com/ask_images/cd661f40c3374245b3b08d4090271c7a.jpg "SOLVED: 6.17 Write a MATLAB code to solve the diffusion equation dx^2 over the domain x ∈ [0, 1] subject to dc/dx(0,x) = d^2c/dx^2(0,x) = 0 (0) for the (dimensionless) reaction rate")
SOLVED: 6.17 Write a MATLAB code to solve the diffusion equation dx^2 over the domain x ∈ [0, 1] subject to dc/dx(0,x) = d^2c/dx^2(0,x) = 0 (0) for the (dimensionless) reaction rate
Diffusion Equation - Two Different Media
Numerical solution of equations of the diffusion type with diffusivity concentration-dependent - Transactions of the Faraday Society (RSC Publishing)
The Advection Diffusion Equation - YouTube
Use a change of variables and the solution to problem | Chegg.com
An example 1-d solution of the diffusion equation
Solving the Convection-Diffusion Equation for this Pipe with a Heat Sink
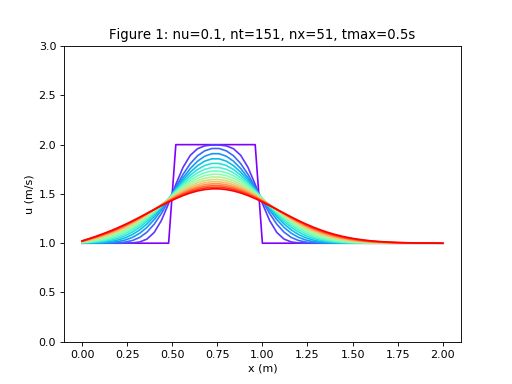
fluid mechanics - Analytical solution for the 1D convection-diffusion equation - Engineering Stack Exchange
Solution to the Diffusion Equation
SOLVED: Given the reaction-diffusion equation: ∂u/∂t = 0.2∂²u/∂x² + 1.1u + 0.4x² 0 < t < 1, 0 < x < 1 (1) with the initial condition: u(x,0) = x + e²
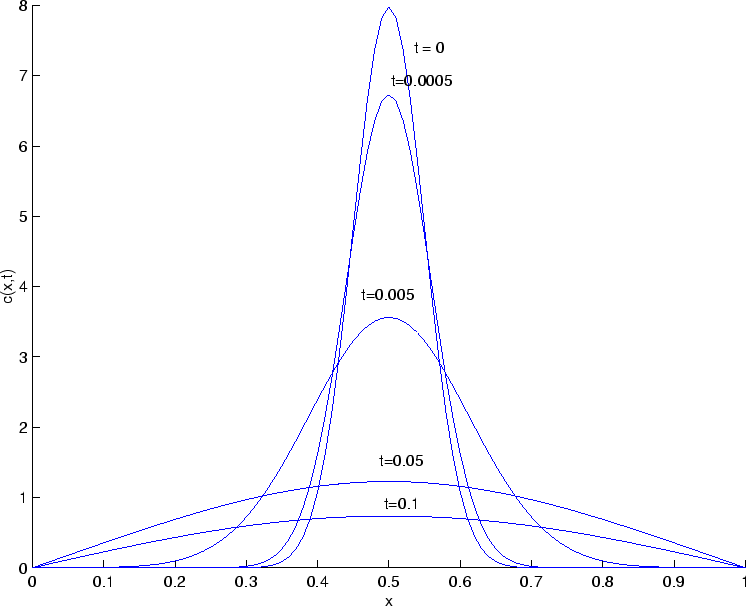
python - Plotting the solution of diffusion equation for multiple times using SciPy - Stack Overflow
SOLVED: Solving the Diffusion Equation Consider the diffusion equation: ∂u ∂t = D ∂²u ∂x² for r ∈ (0,1) and t > 0, subject to the boundary conditions: ∂u ∂x (0,t >
